Exoplanetology: Exoplanets & Exomoons

Empirical Stability Criteria For 3D Hierarchical Triple Systems I: Circumbinary Planets

By Keith Cowing
Status Report
astro-ph.EP
April 24, 2024
Filed under , , , , ,
Empirical Stability Criteria For 3D Hierarchical Triple Systems I: Circumbinary Planets
Mean and standard deviation of outer vs inner stability borders in units of log10 of the binary semi-major axis. The color scale refers to the binary orbit eccentricity (top left), the planet’s orbital eccentricity (top right), the binary mass ratio (bottom left), and the mutual inclination (bottom right). Stability limits depend strongly on the planetary orbital eccentricity which accounts for most of the variance in the system. Stability borders also show roughly the same sensitivity to the binary star orbital eccentricity, the binary mass ratio as well as the inclination of the system. — astro-ph.EP

In this work we revisit the problem of the dynamical stability of hierarchical triple systems with applications to circumbinary planetary orbits.

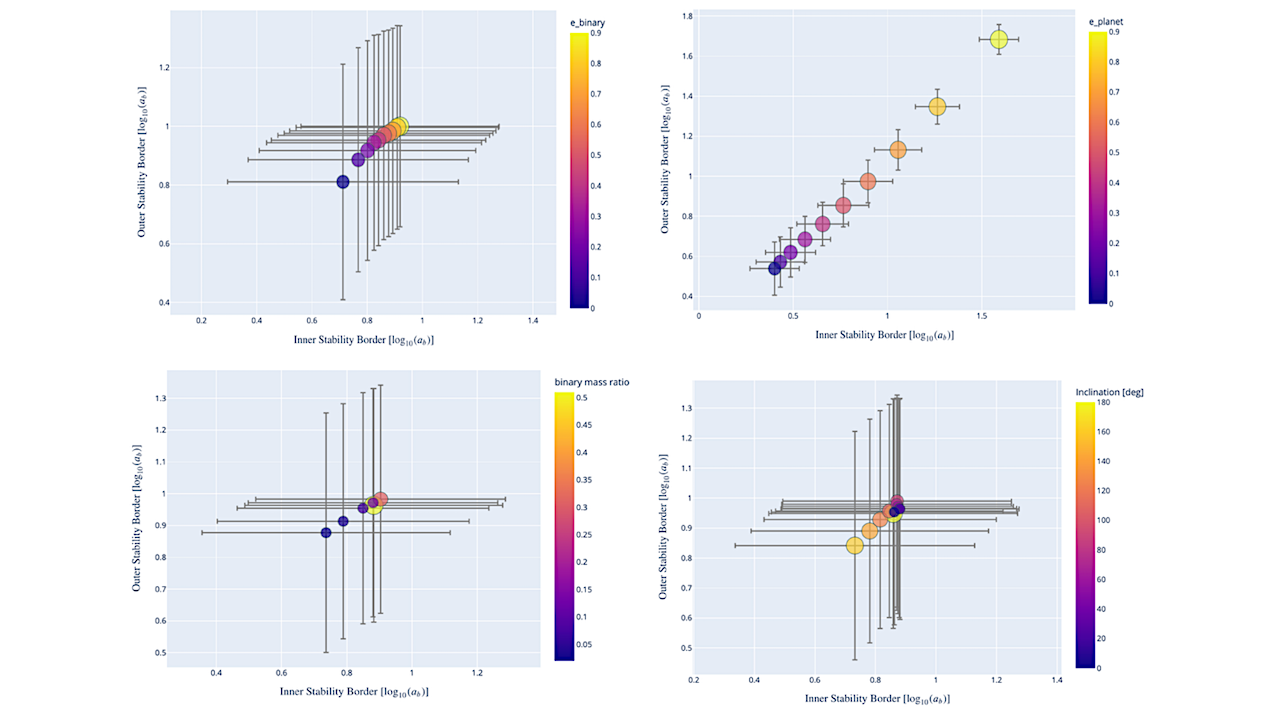
We carry out more than 3 10^8 numerical simulations of planets between the size of Mercury and the lower fusion boundary (13 Jupiter masses) which revolve around the center of mass of a stellar binary over long timescales. For the first time, three dimensional and eccentric planetary orbits are considered. We explore systems with a variety of binary and planetary mass ratios, binary and planetary eccentricities from 0 to 0.9 and orbital mutual inclinations ranging from 0 to 180 degrees. The simulation time is set to 10^6 planetary orbital periods.

We classify the results of those long term numerical integrations into three categories: stable, unstable and mixed. We provide empirical expressions in the form of multidimensional, parameterized fits for the two borders that separate the three dynamical domains.

In addition, we train a machine learning model on our data set in order to have an alternative tool of predicting the stability of circumbinary planets. Both the empirical fits and the machine learning model are tested against randomly generated circumbinary systems with very good results regarding the predictions of orbital stability.

The empirical formulae are also applied to the Kepler and TESS circumbinary systems, confirming the stability of the planets in these systems. Finally, we present a REST API with a web based application for convenient access of our simulation data set.

Nikolaos Georgakarakos, Siegfried Eggl, Mohamad Ali-Dip, Ian Dobbs-Dixon

Comments: Submitted to AJ
Subjects: Earth and Planetary Astrophysics (astro-ph.EP)
Cite as: arXiv:2404.13746 [astro-ph.EP] (or arXiv:2404.13746v1 [astro-ph.EP] for this version)
Submission history
From: Nikolaos Georgakarakos Ph.D.
[v1] Sun, 21 Apr 2024 19:05:02 UTC (9,959 KB)
https://arxiv.org/abs/2404.13746
Astrobiology,

Keith Cowing

Explorers Club Fellow, ex-NASA Space Station Payload manager/space biologist, Away Teams, Journalist, Lapsed climber, Synaesthete, Na’Vi-Jedi-Freman-Buddhist-mix, ASL, Devon Island and Everest Base Camp veteran, (he/him) 🖖🏻

Follow on Twitter
MORE FROM Exoplanetology: Exoplanets & Exomoons