Microlensing Due To Free-Floating Moon-Planet Systems
Gravitational microlensing is a powerful method for detecting and characterizing free-floating planetary-mass objects (FFPs).
FFPs could have exomoons rotating them. In this work, we study the probability of realizing these systems (i.e., free-floating moon-planet ones) through microlensing observations. These systems make mostly close caustic configurations with a considerable finite-source effect.
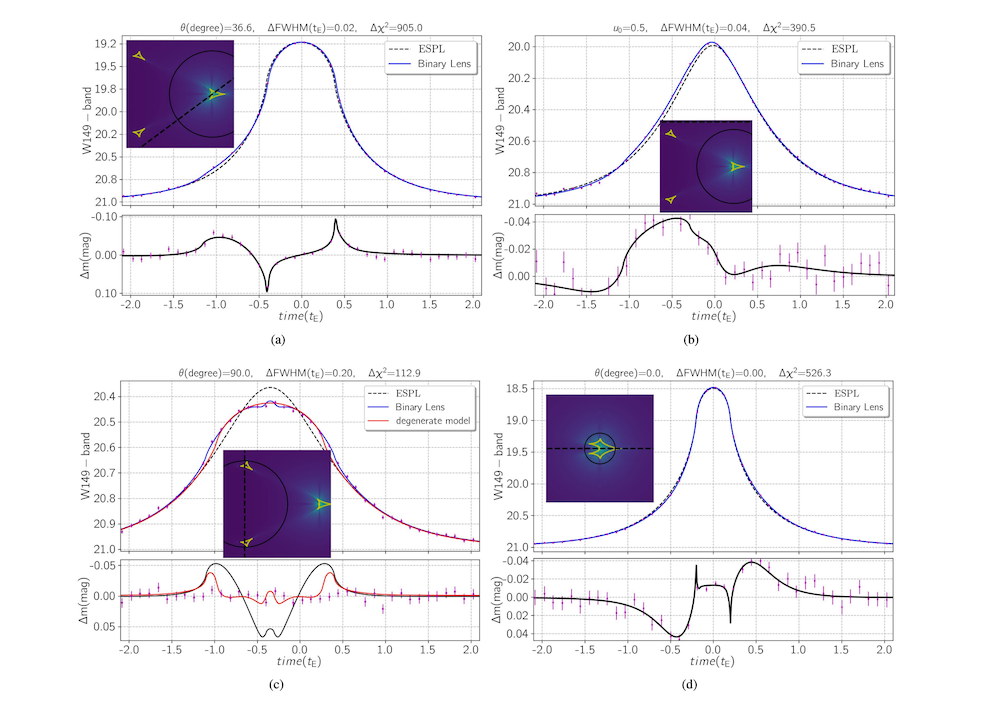
We investigate finite-source microlensing light curves owing to free-floating moon-planet systems. We conclude that crossing planetary caustics causes an extensive extra peak at light curves’ wing that only changes its width if the source star does not cross the central caustic.
If the source trajectory is normal to the moon-planet axis, the moon-induced perturbation has a symmetric shape with respect to the magnification peak, and its light curve is similar to a single-lens one with a higher finite-source effect.
We evaluate the \wfirst~efficiency for realizing moon-induced perturbations, which is [0.002−0.094]% by assuming a log-uniform distribution for moon-planet mass ratio in the range ∈[−9, −2]. The highest detection efficiency (i.e., ≃0.094%) happens for Saturn-mass planets when moon-planet distance is ∼43Rp, where Rp is the Saturn radius.
Enhancing planetary mass extends the event’s time scale and decreases the finite-source effect, but it reduces the projected moon-planet distance normalized to the Einstein radius s(RE) which in turn decreases the size of planetary caustics and takes them away from the host planet’s position in close caustic configurations.
Sedighe Sajadian, Parisa Sangtarash
Comments: 9 pages, 2 tables, 4 figures
Subjects: Earth and Planetary Astrophysics (astro-ph.EP); Astrophysics of Galaxies (astro-ph.GA)
Cite as: arXiv:2302.05230 [astro-ph.EP] (or arXiv:2302.05230v1 [astro-ph.EP] for this version)
Submission history
From: Sedighe Sajadian
[v1] Fri, 10 Feb 2023 12:59:42 UTC (1,049 KB)
https://arxiv.org/abs/2302.05230
Astrobiology