Tides on Lava Worlds: Application to Close-in Exoplanets and the Early Earth-Moon System
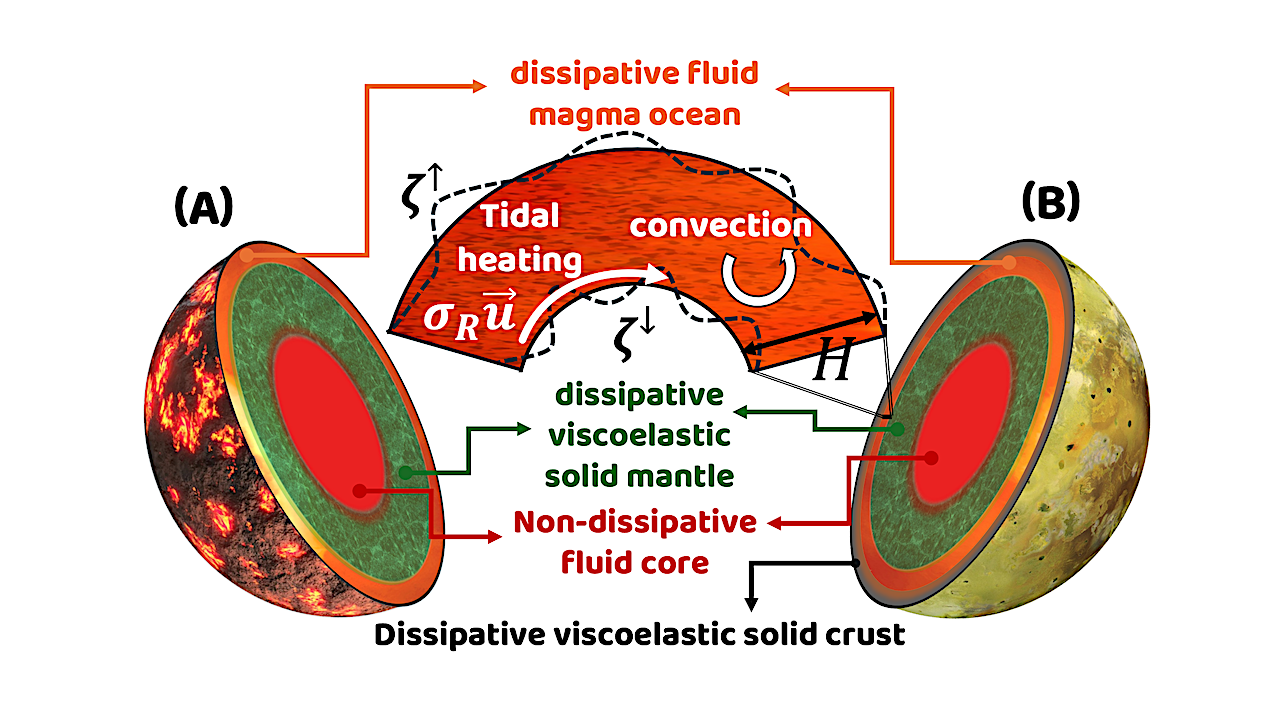
Understanding the physics of planetary magma oceans has been the subject of growing efforts, in light of the increasing abundance of Solar system samples and extrasolar surveys. A rocky planet harboring such an ocean is likely to interact tidally with its host star, planetary companions, or satellites.
To date, however, models of the tidal response and heat generation of magma oceans have been restricted to the framework of weakly viscous solids, ignoring the dynamical fluid behavior of the ocean beyond a critical melt fraction.
Here we provide a handy analytical model that accommodates this phase transition, allowing for a physical estimation of the tidal response of lava worlds. We apply the model in two settings: The tidal history of the early Earth-Moon system in the aftermath of the giant impact; and the tidal interplay between short-period exoplanets and their host stars.
For the former, we show that the fluid behavior of the Earth’s molten surface drives efficient early Lunar recession to ∼25 Earth radii within 104−105 years, in contrast with earlier predictions.
For close-in exoplanets, we report on how their molten surfaces significantly change their spin-orbit dynamics, allowing them to evade spin-orbit resonances and accelerating their track towards tidal synchronization from a Gyr to Myr timescale.
Moreover, we re-evaluate the energy budgets of detected close-in exoplanets, highlighting how the surface thermodynamics of these planets are likely controlled by enhanced, fluid-driven tidal heating, rather than vigorous insolation, and how this regime change substantially alters predictions for their surface temperatures.
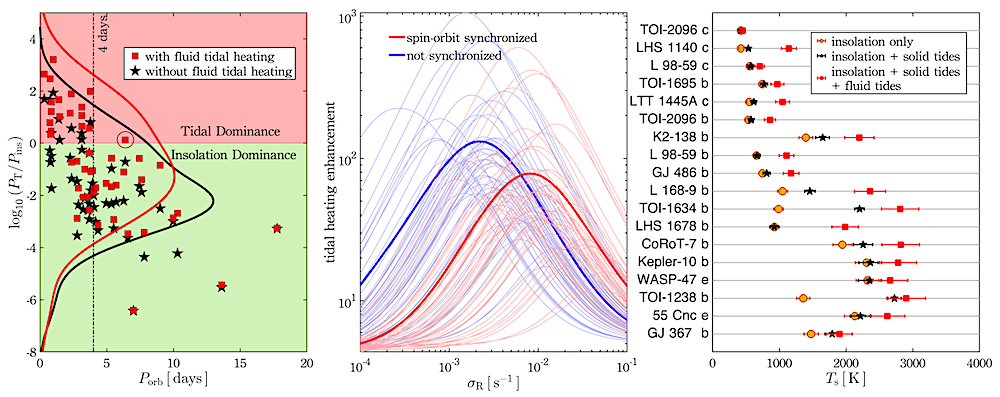
Modeled heating and estimated surface temperatures of close-in exoplanets. Left: Planetary heating via insolation is compared to tidal heating for a population of 59 close-in rocky exoplanets with non-zero eccentricity (see the main text for a description of the population). Tidal heating is computed in two cases: with (red squares) and without (black stars) fluid tides within a surface magma ocean on each planet. Solid curves depict the population distribution in each case. Noticeable is the threshold of Porb = 4 days beyond which all planets are dominated by insolation, with the exception of TOI-2096 c marked by the red circle. Middle: The amplification in tidal heating in the presence of fluid tides as a function of the fluid dissipation frequency, σR, is shown for each planet in the population (light curves), and averaged in the thick curves. The red curves assume spin-orbit synchronization, that is, the presence of eccentricity tides only, while the blue curves relax this assumption and allow for other tidal components. Right: The resulting surface temperature, assuming black body radiation, for a subset of 18 planets that are tidally dominated. Planets are assumed to be tidally locked into spin-orbit synchronization. Uncertainty bars in insolation-driven temperatures reflect the possible variations in planetary Albedo, while uncertainty bars in calculated temperatures allowing for tidal heating reflect variations in the magma ocean thickness and dissipation frequency. — astro-ph.EP
Mohammad Farhat, Pierre Auclair-Desrotour, Gwenaël Boué, Tim Lichtenberg, Jacques Laskar
Comments: 32 pages, 12 figures, accepted for publication in ApJ
Subjects: Earth and Planetary Astrophysics (astro-ph.EP); Atmospheric and Oceanic Physics (physics.ao-ph); Geophysics (physics.geo-ph)
Cite as: arXiv:2412.07285 [astro-ph.EP] (or arXiv:2412.07285v1 [astro-ph.EP] for this version)
https://doi.org/10.48550/arXiv.2412.07285
Focus to learn more
Submission history
From: Mohammad Farhat
[v1] Tue, 10 Dec 2024 08:16:22 UTC (8,410 KB)
https://arxiv.org/abs/2412.07285
Astrobiology