Decoding Geometric Properties in Non-Random Data from First Information-Theoretic Principles

Based on the principles of information theory, measure theory, and theoretical computer science, we introduce a univariate signal deconvolution method with a wide range of applications to coding theory, particularly in zero-knowledge one-way communication channels, such as in deciphering messages from unknown generating sources about which no prior knowledge is available and to which no return message can be sent.

Our multidimensional space reconstruction method from an arbitrary received signal is proven to be agnostic vis-a-vis the encoding-decoding scheme, computation model, programming language, formal theory, the computable (or semi-computable) method of approximation to algorithmic complexity, and any arbitrarily chosen (computable) probability measure of the events.

The method derives from the principles of an approach to Artificial General Intelligence capable of building a general-purpose model of models independent of any arbitrarily assumed prior probability distribution.

We argue that this optimal and universal method of decoding non-random data has applications to signal processing, causal deconvolution, topological and geometric properties encoding, cryptography, and bio- and technosignature detection.

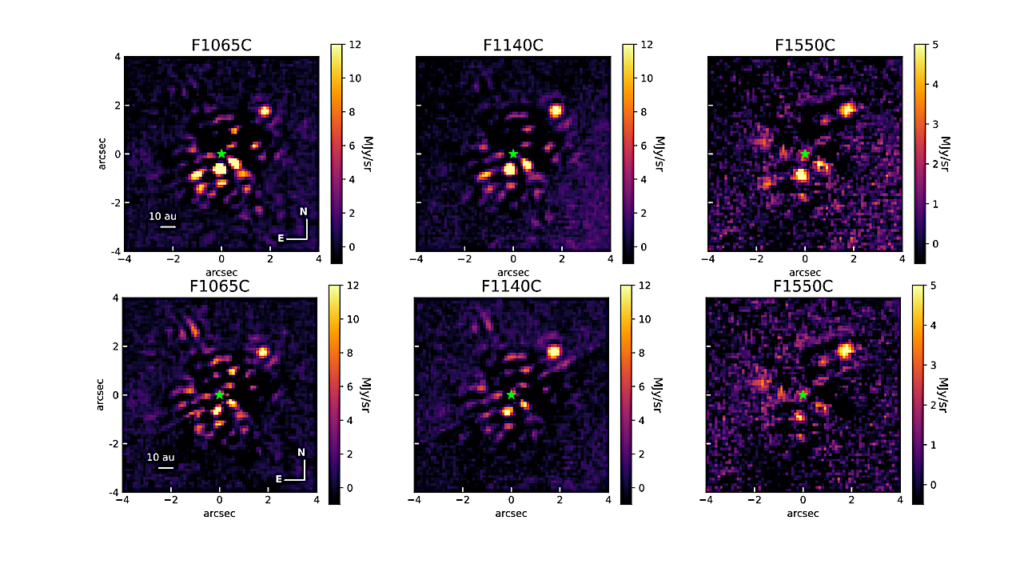
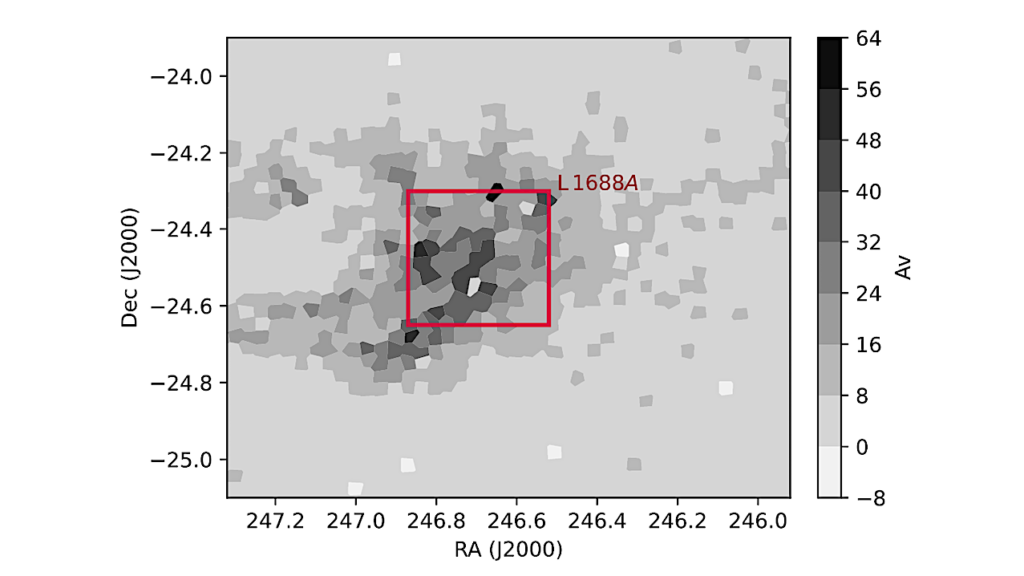
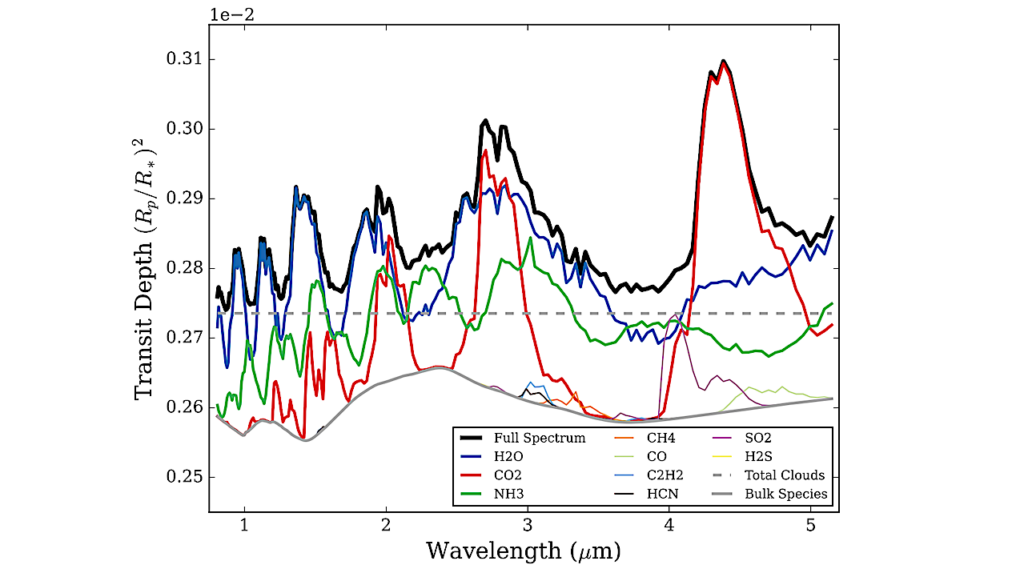
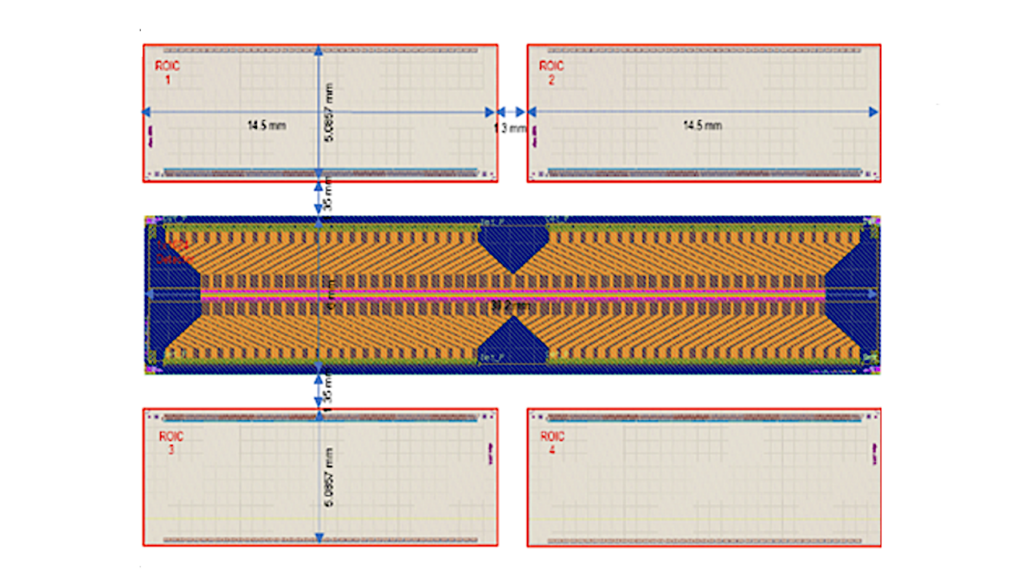
Top left: Most possible partitions result in random-appearing configurations with high corresponding complexity, indicating measurable randomness. Bottom: Some partitions will approximate the originally encoded meaning (third from the right). Other configurations result in images with higher complexity values. This sequence of images shows the images in the approximate vicinity of the correct bidimensional configuration (i.e., partition) and illustrates fast convergence to low complexity. Top right: By using different information indexes across different configurations, a downward-pointing spike will indicate message (image) configurations that correspond to low-complexity image(s). This allows a prior-knowledge-agnostic and objective method to infer a message’s original encoding. Of the various measures, BDM, combining classical information (entropy) for long ranges and a measure motivated by algorithmic probability for short ranges, is the most sensitive and accurate in this regard. Traditional compression and entropy also indicate the right configuration amongst the top spiking candidates. The ratio of noise-to-signal was amplified in favour of the hidden structure by multiplying the original image size by 6 for both length and height. — cs.CL

Hector Zenil, Felipe S. Abrahão

Comments: arXiv:2303.16045 is based on this paper. arXiv admin note: substantial text overlap with arXiv:2303.16045
Subjects: Information Theory (cs.IT); Computation and Language (cs.CL); Cryptography and Security (cs.CR); Information Retrieval (cs.IR); Statistics Theory (math.ST)
Cite as: arXiv:2405.07803 [cs.IT] (or arXiv:2405.07803v2 [cs.IT] for this version)
https://doi.org/10.48550/arXiv.2405.07803
Focus to learn more
Submission history
From: Felipe S. Abrahão
[v1] Mon, 13 May 2024 14:45:08 UTC (2,251 KB)
[v2] Sat, 18 May 2024 01:24:24 UTC (10,146 KB)
https://arxiv.org/abs/2405.07803
Astrobiology, SETI,