Gaia - Planetary Perspectives

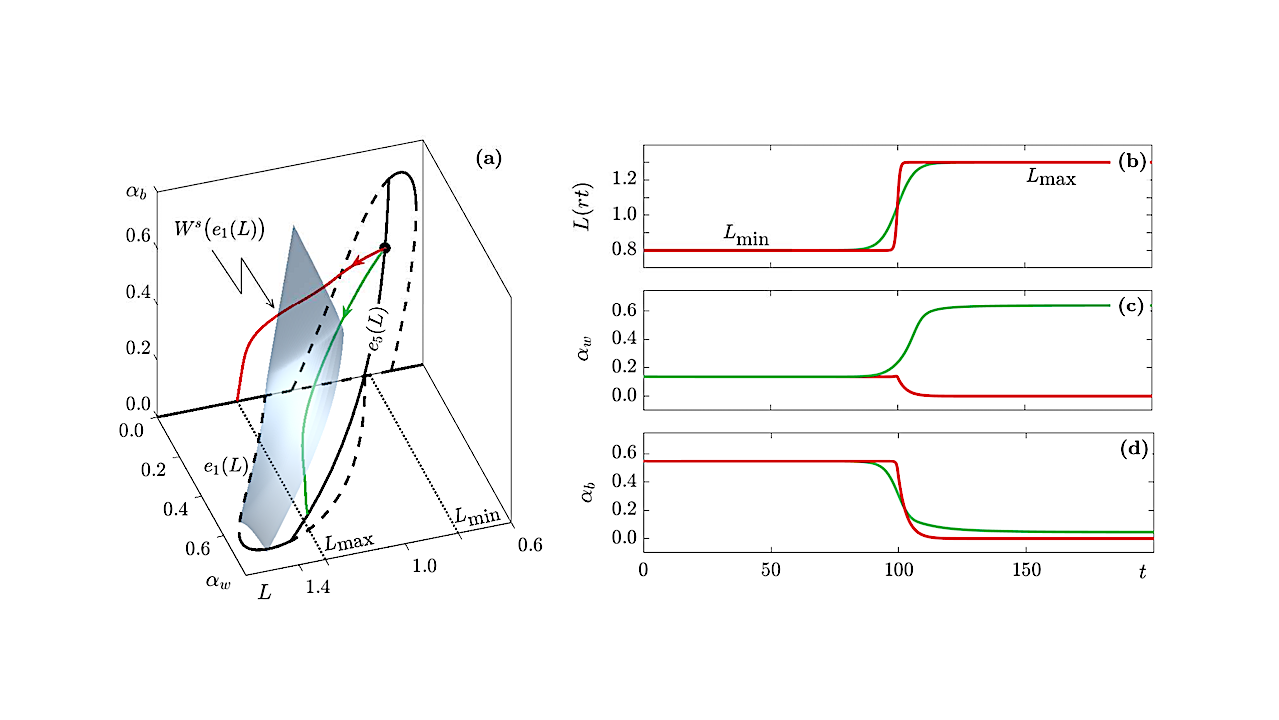
Rate-induced Biosphere Collapse In The Daisyworld Model

By Keith Cowing

Status Report

astro-ph.EP

October 8, 2024

Filed under astro-ph.EP, biodiversity, biosphere, Daisyworld, ecology, ecosystem, extinction, habitability, rate-induced tipping

Rate-induced Biosphere Collapse In The Daisyworld Model — Rate-induced tipping towards extinction in the Daisyworld model. We initialise the system at the coexistence equilibrium (e5) with a value of L = Lmin. Then, we ramp L towards some new value Lmax, at a speed determined by a dimensionless rate parameter r. Panel (b) shows time series of L(rt), while panels (c) and (d) show time series of αw and αb. When the change is slow enough (green, r = 0.5), the biosphere survives; when it is too fast (red, r = 1), the biosphere collapses. This occurs because the system can enter the basin of attraction of the “dead planet” state, e0, if the change in L is fast enough. The threshold for entering this basin of attraction is the stable manifold of the saddle equilibrium e1 (see also Figure 5 and panel f of Figure 1). In the space of αw,αb, and L, the threshold becomes a two dimensional surface Ws (e1(L)): trajectories which cross it are precisely those which tip. This is shown in panel (a). — astro-ph.EP

There is much interest in the phenomenon of rate-induced tipping, where a system changes abruptly when forcings change faster than some critical rate. Here, we demonstrate and analyse rate-induced tipping in the classic “Daisyworld” model.

The Daisyworld model considers a hypothetical planet inhabited only by two species of daisies with different reflectivities, and is notable because the daisies lead to an emergent “regulation” of the planet’s temperature. The model serves as a useful thought experiment regarding the co-evolution of life and the global environment, and has been widely used in the teaching of Earth system science.

We show that sufficiently fast changes in insolation (i.e. incoming sunlight) can cause life on Daisyworld to go extinct, even if life could in principle survive at any fixed insolation value among those encountered. Mathematically, this occurs due to the fact that the solution of the forced (nonautonomous) system crosses the stable manifold of a saddle point for the frozen (autonomous) system.

The new discovery of rate-induced tipping in such a classic, simple, and well-studied model provides further supporting evidence that rate-induced tipping — and indeed, rate-induced collapse — may be common in a wide range of systems.

Constantin W. Arnscheidt, Hassan Alkhayuon

Subjects: Dynamical Systems (math.DS); Earth and Planetary Astrophysics (astro-ph.EP); Populations and Evolution (q-bio.PE)
Cite as: arXiv:2410.00043 [math.DS] (or arXiv:2410.00043v1 [math.DS] for this version)
https://doi.org/10.48550/arXiv.2410.00043
Focus to learn more
Submission history
From: Constantin Arnscheidt
[v1] Fri, 27 Sep 2024 17:34:22 UTC (567 KB)
https://arxiv.org/abs/2410.00043
Astrobiology

Keith Cowing

Explorers Club Fellow, ex-NASA Space Station Payload manager/space biologist, Away Teams, Journalist, Lapsed climber, Synaesthete, Na’Vi-Jedi-Freman-Buddhist-mix, ASL, Devon Island and Everest Base Camp veteran, (he/him) 🖖🏻

Follow on Twitter