Habitable Zones & Global Climate

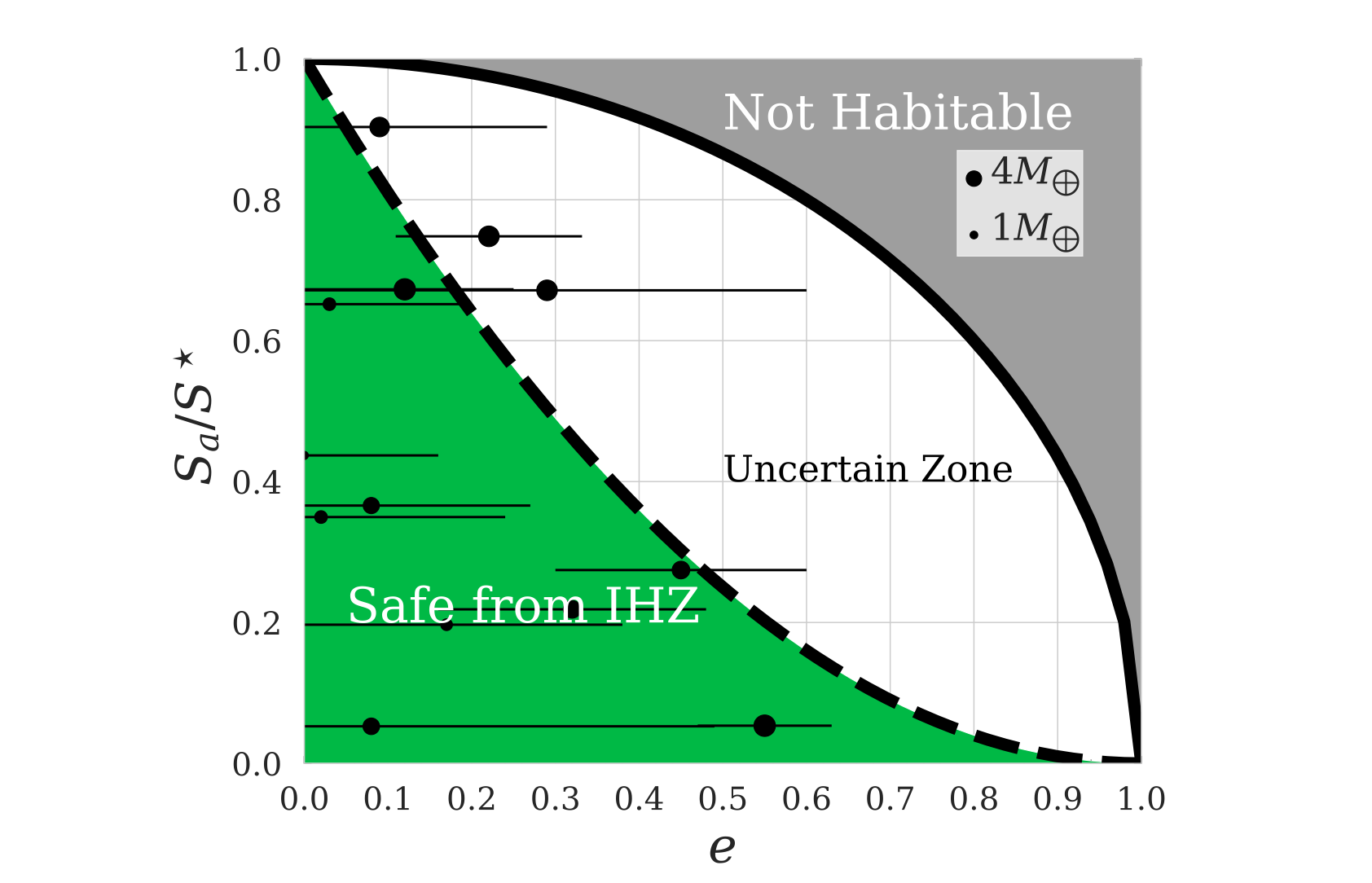
Inner Habitable Zone Boundary For Eccentric Exoplanets

By Keith Cowing
Press Release
astro-ph.EP
November 16, 2022
Filed under , , , ,
Inner Habitable Zone Boundary For Eccentric Exoplanets
Stellar flux and eccentricity of observed exoplanets with masses M < 8M⊕ (NASA Exoplanet Science Institute 2020). Sa is the stellar flux at the semimajor axis of the orbit and S ? is the critical stellar flux of the IHZ for a circular orbit, for which we use the moist greenhouse limit from Kopparapu et al. (2013). The thick solid black curve represents the mean-stellar flux limit on the IHZ. If Sa/S? planet is above this curve a planet is not habitable (Not Habitable). The dashed black curve represents the maximum-stellar flux limit on the IHZ. If Sa/S? is lower than this limit, a planet will not experience a moist or runaway greenhouse (Safe from IHZ). For planets in the region in between the limits (Uncertain Zone), climate calculations involving the time evolution of the surface temperature are necessary to determine planetary habitability. The horizontal bars represent the uncertainties of the observed eccentricities. -- astro-ph.EP

The climate of a planet can be strongly affected by its eccentricity due to variations in the stellar flux.

There are two limits for the dependence of the inner habitable zone boundary (IHZ) on eccentricity: (1) the mean-stellar flux approximation (SIHZ∝1−e2‾‾‾‾‾‾√), in which the temperature is approximately constant throughout the orbit, and (2) the maximum-stellar flux approximation (SIHZ∝(1−e)2), in which the temperature adjusts instantaneously to the stellar flux.

Which limit is appropriate is determined by the dimensionless parameter Π=CBP, where C is the heat capacity of the planet, P is the orbital period, and B=∂Ω∂Ts, where Ω is the outgoing longwave radiation and Ts is the surface temperature. We use the Buckingham Π theorem to derive an analytical function for the IHZ in terms of eccentricity and Π. We then build a time-dependent energy balance model to resolve the surface temperature evolution and constrain our analytical result.

We find that Π must be greater than about ∼1 for the mean-stellar flux approximation to be nearly exact and less than about ∼0.01 for the maximum-stellar flux approximation to be nearly exact. In addition to assuming a constant heat capacity, we also consider the effective heat capacity including latent heat (evaporation and precipitation). We find that for planets with an Earth-like ocean, the IHZ should follow the mean-stellar flux limit for all eccentricities. This work will aid in the prioritization of potentially habitable exoplanets with non-zero eccentricity for follow-up characterization.

Xuan Ji, Nora Bailey, Daniel Fabrycky, Edwin S. Kite, Jonathan H. Jiang, Dorian S. Abbot

Comments: Submitted to ApJL
Subjects: Earth and Planetary Astrophysics (astro-ph.EP)
Cite as: arXiv:2211.07883 [astro-ph.EP] (or arXiv:2211.07883v1 [astro-ph.EP] for this version)
https://doi.org/10.48550/arXiv.2211.07883
Focus to learn more
Submission history
From: Xuan Ji
[v1] Tue, 15 Nov 2022 04:17:31 UTC (273 KB)
https://arxiv.org/abs/2211.07883
Astrobiology

Keith Cowing

Explorers Club Fellow, ex-NASA Space Station Payload manager/space biologist, Away Teams, Journalist, Lapsed climber, Synaesthete, Na’Vi-Jedi-Freman-Buddhist-mix, ASL, Devon Island and Everest Base Camp veteran, (he/him) 🖖🏻

Follow on Twitter
MORE FROM Habitable Zones & Global Climate